Lagrange Punkte

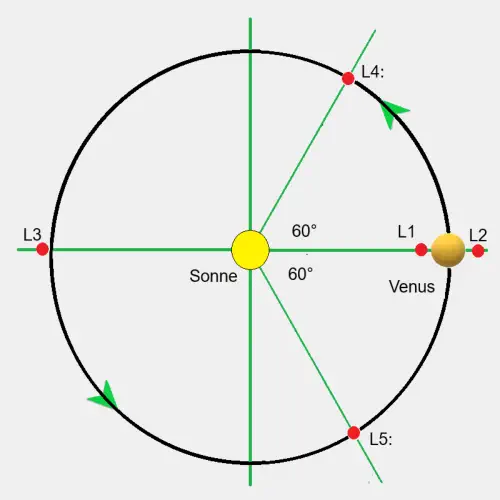
Analyse des Dreikörperproblems (Louis de Lagrange) - Alle Punkte L1 ... L5 liegen in einer Ebene - L1, L2 und L3 liegen auf einer Verbindungslinie - Berechnung des Massenverhältnis nach Lagrange: MV = ( 25 + √ 621 ) / 2 ≈ 24,96 - L4 Masse M3 << M1 * MV und M3 << M2 * MV M3, M2, M1 ergeben ein gleichseitiges Dreck 60° - L5 Masse M4 << M1 * MV und M4 << M2 * MV M4, M2, M1 ergeben ein gleichseitiges Dreck 60° - S Systemschwerpukt M1 ... M4

Da - Durchmesser Äquator Dp - Durchmesser Pol Dm - mittlerer Durchmesser Stand 2026-01-11

AE - 149.597.870,7 km GH - Große Halbachse Siderisches Jahr - 365,256 Tage

In den Punkten L4 und L5 umrunden die Massen M3 oder M4 die Zentralmasse M1 ohne eigenen Antrieb. Der Abstand von 60° zur Masse M2 bleibt dabei erhalten.